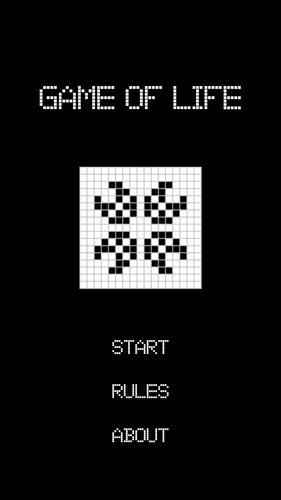
Conway's Game of Life
康威(Conway)的《人生游戏》(Game of Life)是数学家约翰·康威(John Conway)在1970年引人入胜的创作,是蜂窝自动机的一个典型例子。该游戏在无限的二维矩形网格上展开,每个细胞都可以在两个状态之一中:活着或死亡。游戏的演变通过世代发展,每个单元格在下一代中的状态取决于其八个相邻单元格的当前状态 - 这些细胞的当前状态是水平,垂直或对角线的。
游戏以初始模式开头,代表第一代。随后的世代通过同时应用一组规则在网格上的每个单元格中进化。这些规则控制了细胞的出生和死亡,塑造了随着时间的流逝而出现的动态模式。核心规则很简单,但导致了复杂的结果:
- 如果有2或3个活着的邻居,一个活细胞可以生存到下一代。
- 只有在有3个活着的邻居时,一个死细胞才能在下一代中生成。
康威(Conway)在解决这些规则之前进行了各种规则集,这些规则集在两个极端之间进行了微妙的平衡:导致种群迅速减少的规则和导致整个网格中未经检查的扩张的规则。这种平衡至关重要,因为在这个边界上出现了最复杂和最迷人的模式,反映了其他混乱系统中观察到的原理。
最新版本0.2.2中的新功能
最后一次更新于2024年8月3日更新,最新版本的康威人生游戏游戏继续以永恒的吸引力和无限的可能性吸引和挑战爱好者。
Conway's Game of Life
康威(Conway)的《人生游戏》(Game of Life)是数学家约翰·康威(John Conway)在1970年引人入胜的创作,是蜂窝自动机的一个典型例子。该游戏在无限的二维矩形网格上展开,每个细胞都可以在两个状态之一中:活着或死亡。游戏的演变通过世代发展,每个单元格在下一代中的状态取决于其八个相邻单元格的当前状态 - 这些细胞的当前状态是水平,垂直或对角线的。
游戏以初始模式开头,代表第一代。随后的世代通过同时应用一组规则在网格上的每个单元格中进化。这些规则控制了细胞的出生和死亡,塑造了随着时间的流逝而出现的动态模式。核心规则很简单,但导致了复杂的结果:
- 如果有2或3个活着的邻居,一个活细胞可以生存到下一代。
- 只有在有3个活着的邻居时,一个死细胞才能在下一代中生成。
康威(Conway)在解决这些规则之前进行了各种规则集,这些规则集在两个极端之间进行了微妙的平衡:导致种群迅速减少的规则和导致整个网格中未经检查的扩张的规则。这种平衡至关重要,因为在这个边界上出现了最复杂和最迷人的模式,反映了其他混乱系统中观察到的原理。
最新版本0.2.2中的新功能
最后一次更新于2024年8月3日更新,最新版本的康威人生游戏游戏继续以永恒的吸引力和无限的可能性吸引和挑战爱好者。