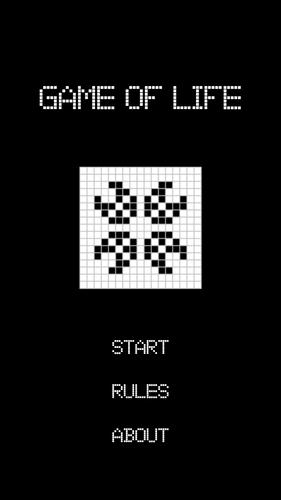
Conway's Game of Life, a fascinating creation by mathematician John Conway in 1970, stands as a prime example of a cellular automaton. This game unfolds on an infinite two-dimensional rectangular grid of cells, where each cell can be in one of two states: alive or dead. The evolution of the game progresses through generations, with each cell's status in the next generation determined by the current state of its eight neighboring cells—those touching it horizontally, vertically, or diagonally.

The game begins with an initial pattern, which represents the first generation. Subsequent generations evolve by applying a set of rules simultaneously to every cell on the grid. These rules govern the birth and death of cells, shaping the dynamic patterns that emerge over time. The core rules are straightforward yet lead to complex outcomes:

• A living cell survives to the next generation if it has exactly 2 or 3 living neighbors.
• A dead cell comes to life in the next generation only if it has precisely 3 living neighbors.

Conway experimented with various rule sets before settling on these, which are delicately balanced between two extremes: rules that cause populations to rapidly dwindle and those that lead to unchecked expansion across the grid. This balance is crucial, as it is at this boundary where the most intricate and captivating patterns emerge, reflecting the principles observed in other chaotic systems.

What's New in the Latest Version 0.2.2

Last updated on Aug 3, 2024, the latest version of Conway's Game of Life continues to captivate and challenge enthusiasts with its timeless appeal and infinite possibilities.