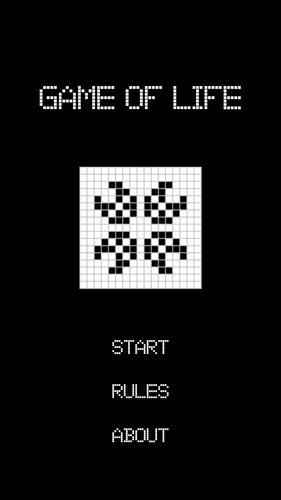
Conway's Game of Life, un'affascinante creazione del matematico John Conway nel 1970, si rappresenta un primo esempio di automobile cellulare. Questo gioco si svolge su una griglia rettangolare rettangolare bidimensionale infinita, dove ogni cellula può essere in uno dei due stati: vivo o morto. L'evoluzione del gioco avanza attraverso le generazioni, con lo stato di ogni cella nella generazione successiva determinata dallo stato attuale delle sue otto celle vicine, che lo toccano in orizzontale, verticalmente o in diagonale.

Il gioco inizia con uno schema iniziale, che rappresenta la prima generazione. Le generazioni successive si evolvono applicando una serie di regole contemporaneamente a ogni cella sulla griglia. Queste regole regolano la nascita e la morte delle cellule, modellando i modelli dinamici che emergono nel tempo. Le regole fondamentali sono semplici ma portano a risultati complessi:

• Una cellula vivente sopravvive alla prossima generazione se ha esattamente 2 o 3 vicini viventi.
• Una cellula morta prende vita nella prossima generazione solo se ha precisamente 3 vicini viventi.

Conway ha sperimentato vari set di regole prima di stabilirsi su questi, che sono delicatamente bilanciati tra due estremi: regole che fanno ridere rapidamente le popolazioni e quelle che portano a un'espansione incontrollata attraverso la griglia. Questo equilibrio è cruciale, come è a questo confine in cui emergono i modelli più intricati e accattivanti, riflettendo i principi osservati in altri sistemi caotici.

Novità nell'ultima versione 0.2.2

Ultimo aggiornato il 3 agosto 2024, l'ultima versione di Conway's Game of Life continua a affascinare e sfidare gli appassionati con il suo fascino senza tempo e le sue infinite possibilità.